|
Cómo construir un domo
Un domo is an almost spherical structure based
on a network of struts arranged on great circles (geodesics)
lying on the surface of a sphere. The geodesics intersect
to form triangular elements that create local triangular rigidity
and distribute the stress. It is the only man made structure
that gets proportionally stronger as it increases in size.
Advantages of domes
Domes are very strong, and get stronger the larger they get.
The basic structure can be erected very quickly from lightweight
pieces by a small crew. Domes as large as fifty meters have
been constructed in the wilderness from rough materials without
a crane. The dome is also aerodynamic, so it withstands considerable
wind loads, such as those created by hurricanes. Solar heating
is possible by placing an arc of windows across the dome:
the more heating needed the wider the arc should be, to encompass
more of the year.
Today there are many companies that sell both dome plans
and frame material with instructions designed simply enough
for owners to build themselves, and many do to make the net
cost lower than standard construction homes. Construction
techniques have improved based on real world feedback over
sixty years and many newer dome homes can resolve nearly all
of the disadvantages below that were more true of the early
dome homes.
  El
domo es una cúpula geodésica. Estos son, normalmente,
semiesferas hechas con triángulos que forman pentágonos
y hexágonos. La primera cúpula geodésica
fue construida por el Dr. Walter Bauersfeld en 1922. Buckminster
Fuller obtubo la primera patente para una en 1951. Este sistema
es bueno para hacer edificios. Son inexpresivos, duros, resistentes
y de fácil construcción y ensamblaje. Aquí
os mostramos una forma de construirte tu propio domo con tubos
de acero.
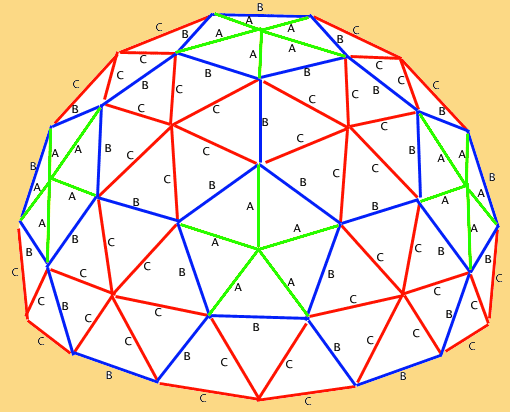
La propuesta es para un domo de 10 metros de diámetro.
The edge lengths listed above can be measured in any way you
like (including inches or centemeters); what is important
is to preserve their relationship. For example, if you make
edge A 34.86 centemeters long, make edge B 40.35 centemeters
long and edge C 41.24 centemeters long. This dome has a radius
of one: that is, to make a dome where the distance from the
center to the outside is equal to one (one meter, one mile,
etc.) you will use panels that are divisions of one by these
amounts. So if you know you want a dome with a diameter of
one, you know you need an A strut that is one divided by .3486.
You can also make the triangles by their angles. Do you need
to measure an AA angle that is exactly 60.708416 degrees?
Not for this model: measuring to two decimal places should
be enough. The full angle is provided here to show that the
three vertex of the AAB panels and the three vertex of the
CCB panels each add up to 180 degrees.
AA = 60.708416
AB = 58.583164
CC = 60.708416
CB = 58.583164
 
1.
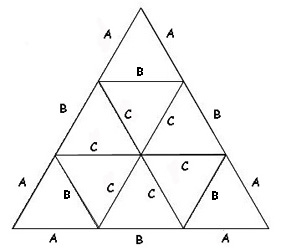
Make seventy five triangles with two C edges and one B edge.
These will be called CCB panels, because they have two C edges
and one B edge. Make thirty triangles with two A edges and
one B edge. Include a foldable flap on each edge so you can
join your triangles with paper fasteners or glue. These will
be called AAB panels, because they have two A edges and one
B edge. You now have 75 CCB panels and 30 AAB panels.
2. Connect
the C edges of six CCB panels to form a hexagon (six-sided
shape); the outer edge of the hexagon should be all B edges.
Make ten hexagons of six CCB panels. If you look close, you
might be able to see that the hexagons are not flat, that
they are a very shallow dome.
3. Are
there some CCB panels left over? Good! You need those too.
Make five half hexagons in which the three B vertex touch
and four of the six C edges touch.
4. Connect
the A edges of five AAB panels to form a pentagon (five-sided
shape); the outer edge of the pentagon should be all B edges.
Make six pentagons of five AAB panels. The pentagons also
form a very shallow dome.
5. This geodesic dome is built from the top outward.
One of the pentagons made of AAB panels is going to be the
top. Take one of the pentagons and connect five hexagons to
it; the B edges of the pentagon are the same length as the
B edges of the hexagons, so that is where they connect. You
should now see that the very shallow domes of the hexagons
and the pentagon form a less shallow dome when put together;
it is starting to look like a 'real' dome already.
6. Take
five pentagons and connect them to the outer edges of the
hexagons. Just like before, the B edges are the ones to connect.
7. Take
six hexagons and connect them to the outer B edges of the
pentagons and the hexagons.
8. Finally,
take the five half hexagons and connect them to the outer
edges of the hexagons.
Congratulations! You have built a geodesic dome! This dome
is 5/8ths of a sphere (a ball), and is a three-frequency dome.
The frequency of a dome is measured by how many edges there
are from the center of one pentagon to the center of another
pentagon. Increasing the frequency of a geodesic dome increases
how spherical (ball-like) the dome is.
Now you can
decorate it. How would it look if it were a house? How would
it look if it were a factory? How would it look under the
ocean or on the moon? Where would the doors go? Where would
the windows go?
If you would
like to make this dome with struts instead of panels, use
the same length ratios to make 30 A struts, 55 B struts and
80 C struts.
The first
geodesic dome was built by Dr. Walter Bauersfeld in 1922.
Buckminster Fuller obtained his first patent for a geodesic
dome in 1951 (patent number 2,682,235). Geodesic domes are
a good way to make buildings. They are inexpensive, strong,
easy to assemble and easy to tear down. They can even be built,
picked up and moved somewhere else. Domes make good temporary
emergency shelters as well as long-term buildings. Perhaps
some day they will be used in outer space, on other planets
or under the ocean. If geodesic domes were made like automobiles
and airplanes are made, on assembly lines in large numbers,
almost everyone in the world today could afford to have a
home.
Copyright © 1998, 1999, 2000, 2001 Trevor Blake (box2321@box2321.com).
All rights reserved. Permission granted to reproduce and distribute
for non-profit and educational use.
First of all, you need this simple formula:
dome radius = strut length/strut factor
which is the same as:
strut length = dome radius * strut factor
| Strut |
Strut factor |
3/8 |
5/8 |
Sphere |
 |
| A |
.34862 |
30 |
30 |
60 |
| B |
.40355 |
40 |
55 |
90 |
| C |
.41241 |
50 |
80 |
120 |
| 4-way connectors |
15 |
15 |
0 |
| 5-way connectors |
6 |
6 |
12 |
| 6-way connectors |
25 |
40 |
80 |
|
SOBRE
ESTA WEB
